Calculus Methods
03 Separating Partial Fractions
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page
1) Completely factor the denominator, and
completely expand the numerator. Each factor in
the denominator should now be either linear or
quadratic.
2) Write an equation with the new fraction on one
side; on the other side, write a sum of fractions:
each fraction will use a constant in the numerator
and a separate factor (from the new fraction in
part 1) as its denominator. If a factor appears more
than
once, (for instance
![]() in
in
![]() ), then you
), then you
will need to use two separate fraction, one for each
power in the factor (for instance
![]() .
.
Also, if the factor in the denominator is quadratic,
then the numerator must be linear.
3) On one side of the equation, you now have a sum
of many fractions. Combine those fractions into a
single fraction and completely expand the
numerator.
4) Since the fractions obtained in steps 1 and 3 are
equal, their numerators must be equal. Also, since
there are variables on each side, the coefficients of
each individual power on each side must be equal.
That means that you can set up a series of
equations. If done properly, you will have the same
number of equations as unknowns.
5) Solve the equations to get the unknowns.
6) Write out the fractions.
Example #1: Separate the following fraction into
partial fractions:
![]()
1) The numerator is already expanded, and the
denominator needs to be factored.
![]()
2)
The factor
![]() occurs twice, so we
will need to
occurs twice, so we
will need to
separate fractions for that factor.
![]()
3)
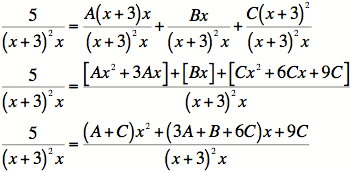
4)

Setting up the three equations:
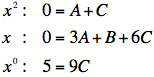
5) Now use your favorite method of solving a
system of equations:
![]()
6)
![]()
Example #2: Separate the following fraction into
partial fractions:
![]()
1) The numerator needs to be expanded and the
denominator needs to be factored.
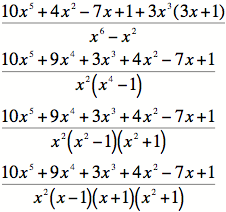
2)
One factor (![]() ) occurs twice, so we
will need to
) occurs twice, so we
will need to
fractions for ![]() . Also, we have
a quadratic factor, so
. Also, we have
a quadratic factor, so
its numerator will be linear.
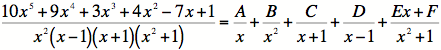
Note that we have six unknowns, so we should end
up with six equations in step 4.
3)
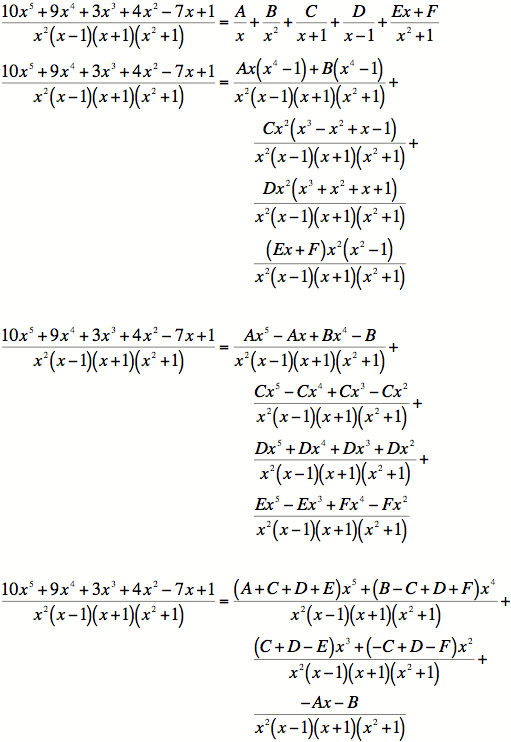
4)
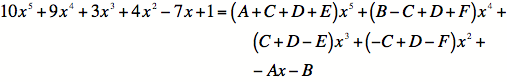
Setting up the 6 equations:
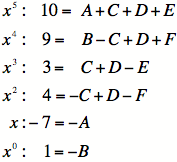
5) Now use your favorite method of solving a
system of equations:
![]()
6)
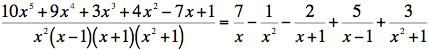
On to Method 04 - Finding Limits
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page