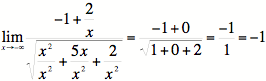Calculus Methods
10 Limits at Infinity
To calculate limits at infinity, one must keep in mind
that 
is "unbounded" or
"undefined" or "no
limit," whereas 
and 
. The reason we
care about the limits at infinity, is that this tells us
how a function behaves as x gets larger or smaller.
1A) If the numerator and denominator both
comprise polynomials, divide the top and the
bottom by the largest power of x.
1B) If there are roots involved, make sure you
know what the largest power it properly. For
instance, for 
, one would
divide the top
and bottom by 
. The trick
to determining what
actually is, you must
know whether you are
taking the limit at infinity or the limit at negative
infinity, because for 
, 
and for 
,
(you can prove this to yourself by
performing a few examples).
2) Take the limit.
3)
and 
are both undefined.
Example
#1: Find 
.
1A)
The largest power of the top or bottom is 
.
Dividing the top and the bottom by that give us:
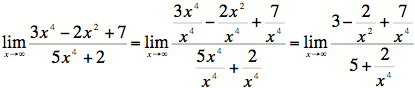
2) Now we can take the limit:
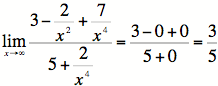
Note that there would be no difference if we were
to take the limit at negative infinity.
Example
#2: Find 
.
1A)
The largest power of the top or bottom is 
.
Dividing the top and the bottom by that give us:
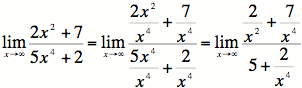
2) Now we can take the limit:
Note that there would be no difference if we were
to take the limit at negative infinity.
Example
#3: Find 
.
1B)
The largest power of the top or bottom is 
(this is the same order as 
). Dividing
the top and
the bottom by that give us:
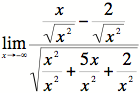
Since
we are looking at negative values for 
,
we
know 
.
Therefore we have:
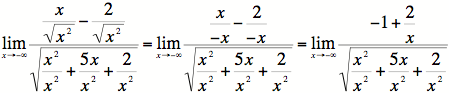
2)
