Calculus Methods
13 Newton's Method
This is a method for finding the zeroes of a function. Is it
useful? Not so much. There are much better methods out
there at this time in history, and any graphing calculator
will do it as well. Why include it, then? Well, it's on the
AP Calculus BC test, so here it is. For a brief, probably
unhelpful derivation of why it works, see lesson 19.
1) A brief sketch might help, but for a complicated function,
this would be time-prohibitive.
2) Find the first derivative of the function.
3) Pick a starting value for x that is anywhere near the actual
zero. The guess doesn't have to be great, but it should be as
good as possible. Call this
starting guess 
.
4)
The next step is to find 
using 
.
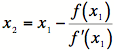5)
Continue along in the same way,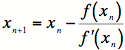 
.
6) The process continues until some tolerance is reached
(
is less
than some value).
7) Repeat for as many zeroes as you need to find!
Example:
Find the roots of 
to within 0.05. Note
that since this is a simple function, we already know that the
answers should
be 
.
1) Let's skip the sketch.
2)
3)
Let's start with 
.
4)
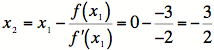
5) 
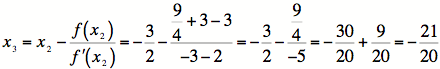
6)
Note that 
, so we are finished
with one
of the zeroes (
). At this
point, however, we would
probably look at the answer and say to ourselves "hey, that
looks a lot like -1, let's try plugging -1 in to the equation to see
if the answer is zero. So using this information, we would
discover
that one of the zeroes occurs at 
.
7) Now we repeat for another zero. Since we are dealing with
a quadratic, we could have two zeroes.
1) We'll still skip the drawing.
2)
3)
.
4)
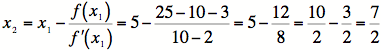
5)
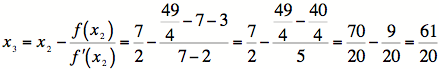
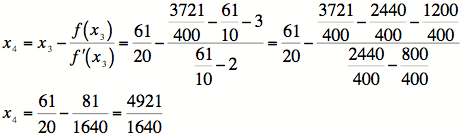
6)
Again, we see that 
and within our
tolerance.
So our final answer is that the two zeroes that we found using
Newton's Method are
and 
,
but we would see
how close these are to whole numbers, and after checking
those numbers in the original equation, we would know that
the two answers are 
and 
.