Calculus Methods
16 u-Substitution
The key is to always look for a function and its derivative.
1) Ask yourself "the big three questions." If the answer to any
of the following is yes, just integrate (seem method 14)!
1A) Is the integrand just a simple polynomial?
1B) Is the integrand just a simple trig function (see
1C) Is the integrand just one over a variable?
2) Since the answers to all of the above questions were all
"no," look for a function and its derivative, both in the
integrand. The derivative does not have to be exact, just good
to a constant. Also, use as much of the "function" part as
possible.
3) Call the "function" part "u."
4) Evaluate du
4A)
Find the derivative, 
.
4B)
Multiply both sides of the equation by 
to
solve
for 
. Make any
adjustments necessary to make the
differential you just found look like the "derivative" part
of the integrand.
5) Rewrite the new integral. Make sure that all occurrences of
x are eliminated from the integral.
5A) If any occurrences of x remain, back-substitute
using your equation for u.
5B) Change the limits of a definite integral! It is okay if
you do not calculate the new limits, but simply call them
"a" and "b."
6) Evaluate your new integral.
7) Back-substitute to get x back into the function, and
evaluate at the limits if working with a definite integral.
Example
#1: Evaluate 
.
1)
This is not a polynomial, simple trig function, or 
.
2)
In this case, the function is 
and the
derivative is 
.
The power of the functions is what matters. We will worry
about making the coefficients right
later. We use 
and not
just 
to get rid of as much of the function
as possible.
3)
4)
Since
we do not need 
in the integrand, but
only
need 
, we divide both sides
by 2.
5)
Everywhere we see 
, we will replace it
with 
.
Everywhere we see 
, we will replace it with 
.
6) This is now a simple integral.
7)
Example
#2: Evaluate 
.
1)
This is not a polynomial, simple trig function, or 
.
2) In this case, I don't see a function and its derivative, so it
seems like I might be stuck. However, we can still try to
perform a substitution. We'll use the most complicated part to
call u.
3)
.
4)
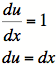
5)
Note
that we replaced 
with 
and 
with
. We
also replaced the limits with generic ones. We still have,
however, an x. From step 3, however, we can eliminate
that x.
6) We can now integrate.
7)
On to Method 17 - Numerical Integration
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page