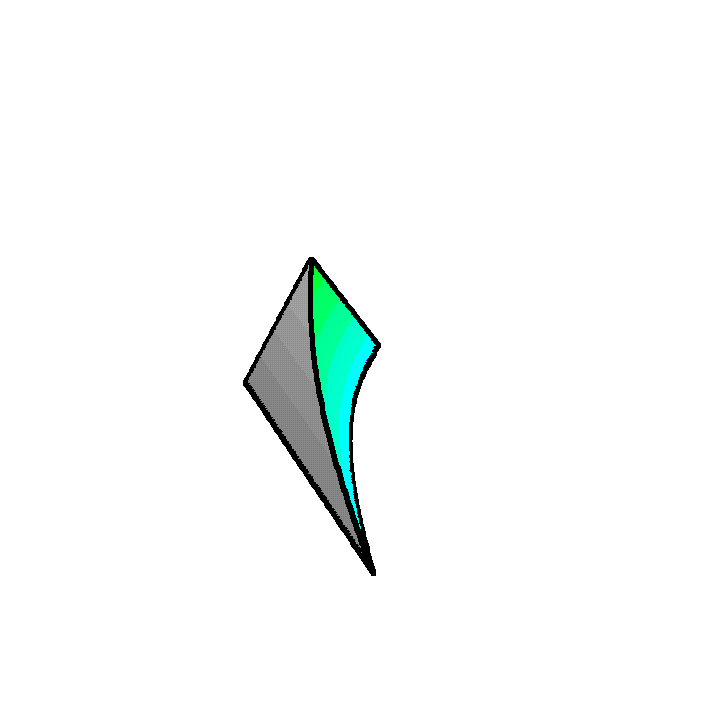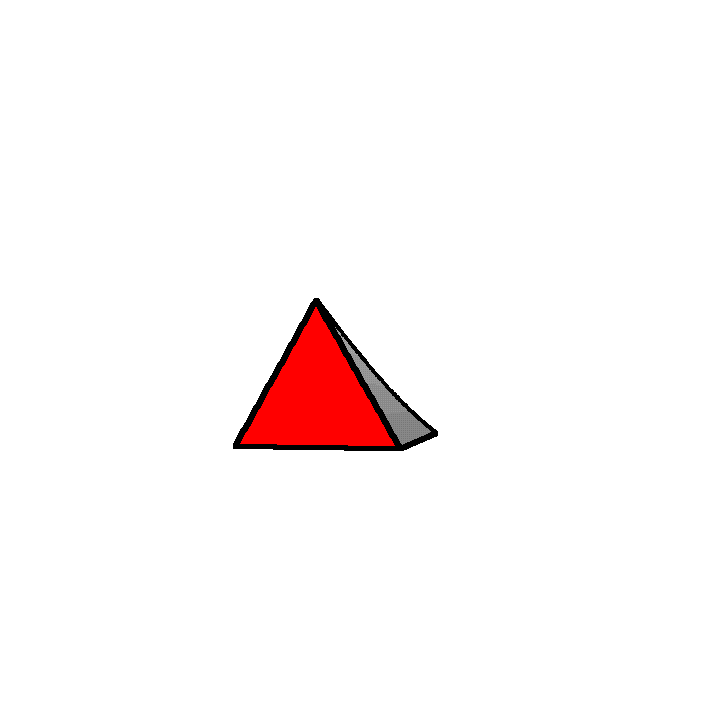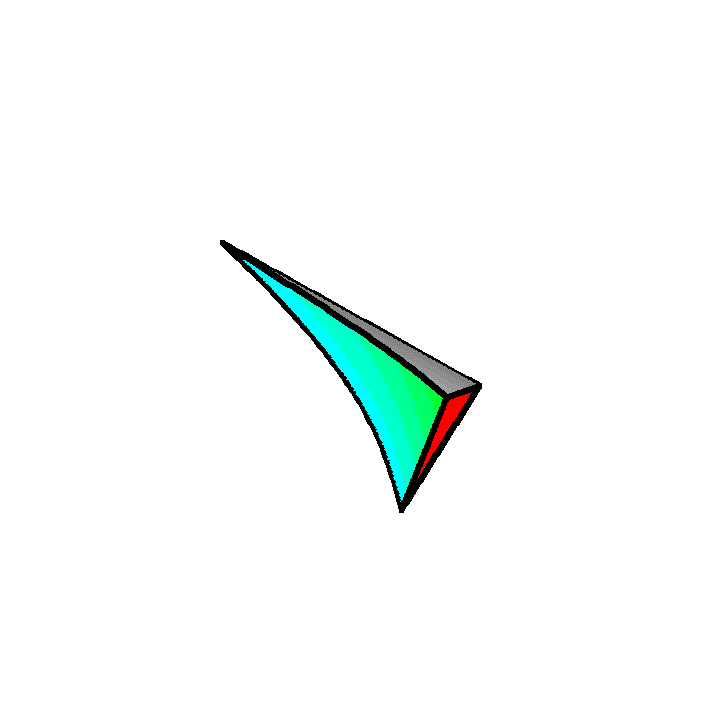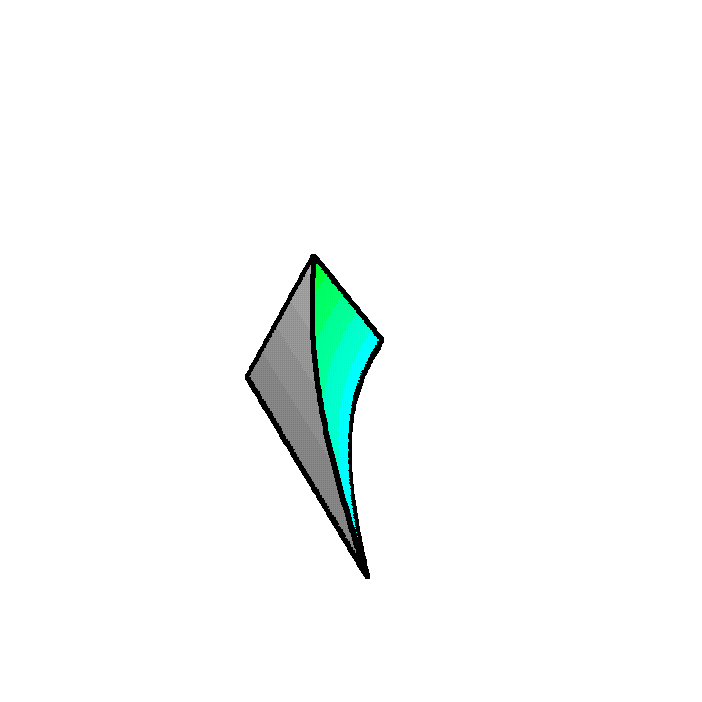This is a companion page to (method 22, Volume). It is an
explanation/demonstration of building up a volume by cross-
section.
Sketching a function like this is NOT required when you perform
such a problem. This is just a guide for this example so you can
see what we're talking about.
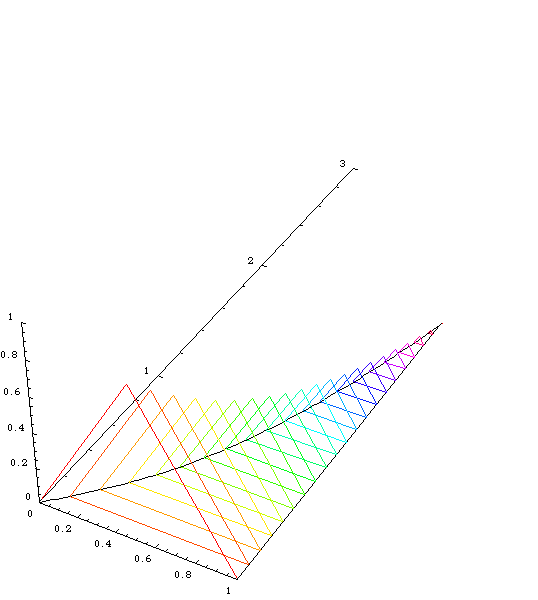
Now, a single cross-section would look like this:
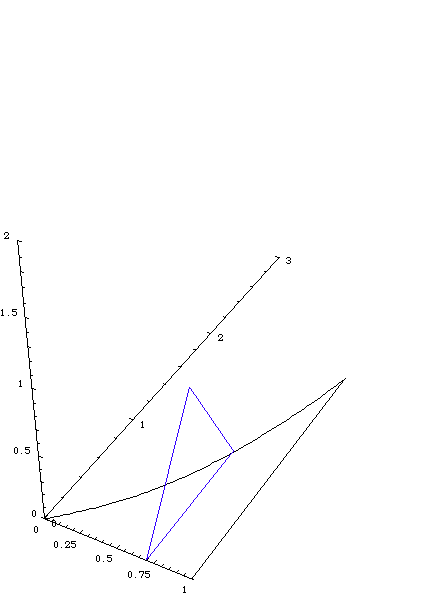
Notice that the x-axis is the one pointing down and to the right
and the y-axis is pointing up and to the right. The z-axis is point
mostly up, but a bit to the left. The cross-section is an equilateral
triangle (in blue), with the base on the region, and the edge of the
3D triangle is perpendicular to the y-axis (and the z-axis).
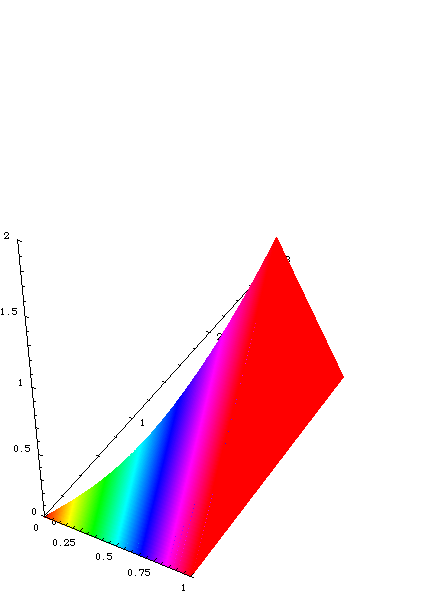
Filling in more of the cross-sections makes it look like this:

In this figure, we can see that each triangle is an equilateral
triangle. That means that the triangles near the "top" are smaller
since the base is small. We also begin to see the shape of the
object.
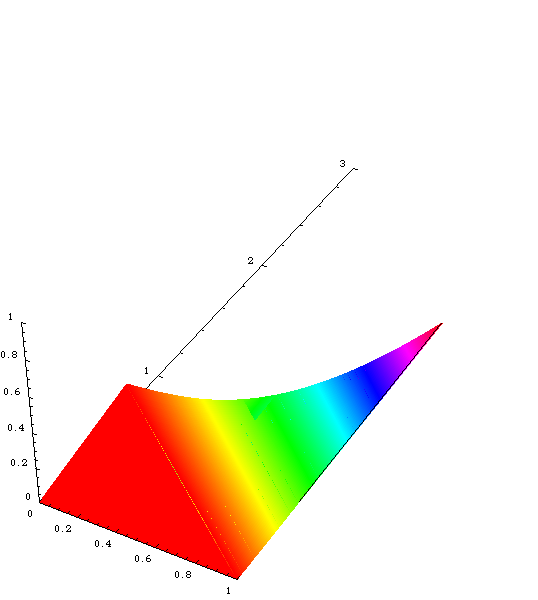
Here it is all filled in:
To get a better view, we could try rotating about, like this:

Finally, note that this is what you get when the cross-sections are
perpendicular to the x-axis. We would get a COMPLETELY
different shape if we use the same equilateral triangle cross-
sections, perpendicular to the y-axis: