Calculus Methods
26 Integration by Parts
1) IF you have already gone through the process of trying to
integrate a function (see method 14, Simple Antiderivatives), then
something you might try is to look for two different functions
within the integrand.
2) Look for a function that has an easy antiderivative. Combine
that function with
the 
, and call the combination 
. Call the
other function 
. You will also then need to CALCULATE 
and 
.
3) Set up the integral equation (see lesson 41 for a derivation):
4) If necessary, repeat the process with the new integrand.
5) If trig functions are involved (or certain other functions) and
you end up with the same integrand with which you started (but
only negative), add the entire integral to both sides to solve for
that integral's value.
TIP:
If 
is involved, use 
so that when you find 
, the 
is no longer in the integrand.
TIP:
If 
is involved, use 
to reduce the power of 
.
TIP:
If 
is involved, it doesn't matter whether
you use it for 
or
for 
, since it is its own derivative and its
own antiderivative.
TIP: Try splitting up functions into parts for which you know the
integral. For
instance, you might spit up 
.
TIP: This is basically a trial & error and experience technique.
Don't forget that u-substitution is ALWAYS the preferable
method!
Example
#1: Evaluate 
.
1) u-substitution does not work since we do not see a function and
its derivative. However, we can then try integration by parts. Since
it does not matter what
we use 
for, and because we
can get rid
of the 
by taking its
derivative, we know what we'll use for 
and
for 
.
2)
3)
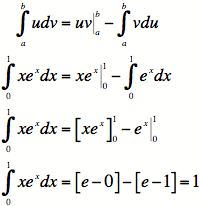
Example
#2: Evaluate 
.
1) This is not a function for which we can use u-sub, so we will
use integration by parts.
2)
3)
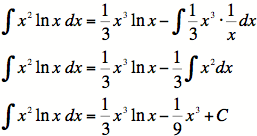
Example
#3: Evaluate 
.
1) We'll use integration by parts!
2) It doesn't matter which we use for either part for this problem!
3)
We don't know how to do the second integral immediately, so
we will do another round of integration by parts.
It looks here as if we might be stuck, but see what happens
when we add that integral to both sides of the equation (we'll
also need to add C since we're done integrating):
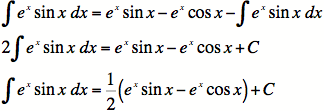
Back to Dr. Nandor's Calculus Methods Page
Back to Dr. Nandor's Calculus Page