Calculus Methods
28 L'Hopital's Rule
You can ONLY use L'Hopital's Rule when you have a
fraction whose LIMITING VALUES in both the numerator
and denominator are 
or
. If numerator is always 0, then
the limit is 0, even if the denominator approaches 0.
For a derivation of L'Hopital's Rule, see lesson 46!
1) Make sure that you are truly dealing with one of the seven
indeterminate forms: 
.
2) If you are dealing
with any of 
, then get it
into a
form that looks like 
or 
.
2A) If 
, divide by one to put it on the bottom.
2B) If 
, combine the fractions into a single
fraction.
2C) If 
, set the limit equal to "L" and take the
log of
both sides of the new equation. At this point, you can pull out
the exponent and you will be left with one
of 
,
, or 
.
3) Take the derivative of the numerator and the derivative of the
denominator separately.
4) Retake the limit. Repeat if necessary.
Example #1: Find 
.
1) When we plug
infinity into the expression, we find 
,
which is
indeed an indeterminate form.
2) Moving the exponential to the bottom, we find:
3) Taking the derivative of the top and bottom separately:
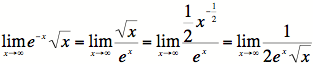
4)
, and we're done.
Example #2: Find the
limit 
.
1) When we plug 0 in
for x, we find we get 
,
which is an
indeterminate form.
2) Combining to get a single fraction, we find
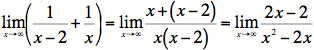
3) Taking the derivative of the numerator and denominator
separately: 
4)
Example #3: Find the
limit 
.
1) When we plug
infinity in for x, we find 
,
and indeterminate form.
2) Already done.
3)
4) We still get 
when we then try to
take the limit, so we will
repeat the process and take the derivative again.
, so the limit is undefined.
Example #4: Find 
1) This is the
indeterminate form 
.
2)
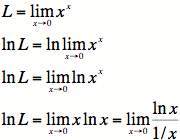
3)
4)
Since
, we know that 
.
So
.
On to Method 29 - Determining Series Convergence