,
Calculus
Lesson
23 The Fundamental Theorem of Calculus
and
The Mean Value Theorem for Integrals
Back to Dr. Nandor's Calculus Notes Page
Back to Dr. Nandor's Calculus Page
FTC: ,
where 
is the
antiderivative of 
and
is continuous on 
Examples: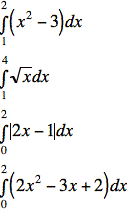 
MVT for integrals: remember that MVT tells us that there was a point on the
curve with the same slope as the average slope.
MVT for integrals tells us that there is a point on the function such that
the area found by 
is
the same as the area under the curve
from 
to 
.
Formally, we say that there exists 
such that 
as long as 
is
continuous on 
.
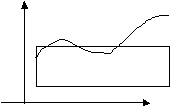
What this is saying is that we can find a rectangle that has the same area as the curve. The
widths are the same. We can find 
such that the height is 
.
 |
Note that there could be more than one value for 
.
We call 
the average
value of the function. Using MVT for integrals, we can then
find
the average value of the function by dividing both sides by 
.
Example: Find the average value of 
on the interval 
.
Example: Find the average value of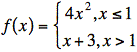 
on the interval 
.
Check for it to be continuous!!!!
Lastly, we have the 2nd Fundamental Theorem of Calculus:
(derive by
using FTC)
This can be interpreted as figuring out how the area is changing!
Let g be a continuous function on an interval,
such that 
and
.
(a) What is the largest possible domain for
?
(b) Write an expression for
.
(c)
(d)
On to Lesson 24 - Integration by Substitution
