Calculus Methods
12 Optimization
This is fairly similar to Related Rates (see method 06)
1) Draw picture (if necessary).
2) Determine the quantity to be optimized.
3) Get any equation involving that quantity.
4) Reduce the equation to a single variable (other
than the quantity to be optimized).
5) Find absolute minimum or absolute maximum
(see method 07), as required by the problem.
6) Answer the question! If the question asks for the
maximum area, give an area as your answer. If the
question asks for dimensions, give dimensions!
Example #1: What is the minimum sum of two
positive numbers such that their product is 64?
1) No picture for this one.
2) We need to maximize the sum, which we'll call S.
3)
An equation for the sum might be 
.
4) We must reduce the equation to one variable, so
we need to find another equation. We know the
product is 64, so we have the equation 
. Using
this equation, we find that 
. This gives us our
equation for S: 
.
5) Finding the critical numbers:
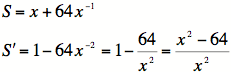
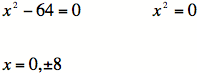
But we are only talking about positive numbers, so
is the only critical number.
To find the absolute maximum, we simply plug in all
critical numbers, and all endpoints. In this case, one
endpoint might be as x approaches 0 and the other
endpoint might be as x approaches infinity.
However, since x cannot be either 0 or infinity,
there are no endpoints. The only option, then, is for
. Given that this is the only point, we
must
check to make sure that it gives us a minimum.
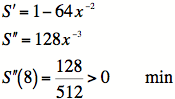
So
IS a minimum.
6) The question asks for the minimum sum:
, so
the minimum sum is 16.
Example #2: A farmer wants to make two pens, one
square and one isosceles right triangle. He has 16 ft
of fencing. How much fencing should he use for the
square in order to minimize his total area?
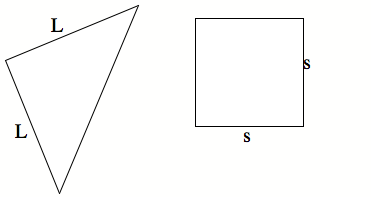1)
2) We are trying to optimize the area, A.
3)
4) We need an equation that relates L and s in order
to eliminate one of them. We still have not used the
total length information. We know that the total
perimeter is 16 ft, so we have the equation
.
If we solve for s, we find
.
Therefore, our equation for area is:
5) Finding our critical numbers:
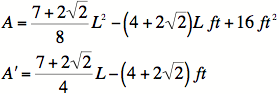
So
we have a critical number 
.
It remains to show that this result gives a minimum
area. The endpoints in this
case are 
(no square)
and 
(no triangle). The area for the
critical point
and endpoints are thus:
The minimum area occurs at our critical number.
6) Since the question asked for the amount of
fencing to be used for the square, we must calculate
s. From the equation relating s and L above, we find
. The amount of fencing used for
the
square, then, is 
.
Something to think about: are the minimum area
and the length of the square at that minimum area
related? Is it coincidence?