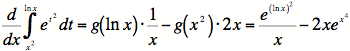Calculus Methods
15 Derivatives of Integrals
Don't become confused! You use this method ONLY when
you are trying to find the derivative of an integral. I don't
teach the Second Fundamental Theorem of Calculus because
it is next to useless (it only applies when the bottom limit is a
constant and the top limit is x). The method outlined here
works every time.
1)
Rename the integrand 
.
2)
Now find the antiderivative, namely 
.
3)
Evaluate 
at the top and bottom
limits.
4) NOW take the derivative with respect to x. Don't forget to
use the chain rule!
5) Back-substitute in for g.
Example
#1: Find 
.
1)
2)
3)
4)
5)
Note for this example that the result is the same as the Second
FTC, because the bottom limit is a constant and the top limit
is simply x.
Also note that the beauty of taking the derivative of an
integral is that you do not have to find an actual closed form
of the antiderivative to do it. In fact, the original integral may
not even be integrable, as in Example #2.
Example
#2: Find 
.
1)
.
2)
3)
4)
5)
