Calculus Methods
20 Finding Inverse Functions
1)
Check to see if 
even has an inverse
(see if 
is one-to-
one (it must pass both the horizontal and vertical line tests)). The
easiest way to do this is to draw a quick sketch and to look at it's
domain.
2)
Solve the equation for 
.
3)
Rewrite the equation such that 
is now
written as 
and all
of the
previous 
s are now written as 
.
4)
Check to make sure that 
. This is not a
necessary step if you have made sure that the function is one-to-
one. However, it is a nice check.
5)
The domain of 
is the range of 
; the domain of 
is
the range of 
. Okay, this is not
really a "step," but it's
something to keep in mind.
Example
#1: If 
has an inverse, find
it.
1) The function is a parabola, so it does not pass the horizontal
line test. The function is not one-to-one, so there is no inverse.
Example
#2: If 
has an inverse, find
it.
1) While this function has a shape similar to the function in
example #1, this function is one-to-one, since it continually
increases over it's entire domain (
, which is always
positive when 
).
2)
3)
Note
that we have two answers for 
:
.
This
is problematic because both 
and 
are supposed to
be one-to-one, so only one of these answers can be correct. We
can fix this, however, by remembering
that the domain of 
is
the range of 
. Since the domain of 
is 
, only
one of the
above functions 
will
actually work. Note that the maximum
value when we use the fraction with "-" in it is when x is as large
as possible (
).
When this happens, that fraction is STILL less
than 
.
The other function must be the correct answer. So
.
Example
#3: If 
has an inverse, find
it.
1)
The function is a strict function of 
,
so it is definitely a
function. The question as to whether it is one-to-one is still up in
the air, however. If nothing else, we can try sketching the function
(see method 11):
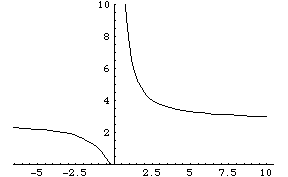
During the sketching process, we find that there is a horizontal
asymptote at 
, so this function does indeed pass both
the
vertical and horizontal line tests.
2)
3)
, which is clearly also a function.
On to Method 21 - Handling ax and logax