Calculus Methods
23 Arc Length
The only thing you really have to remember is the
Pythagorean Theorem: for
coordinates 
, where 
is
the length of the hypotenuse. For a differential length, then,
we can easily see that 
.
1)
Decide whether it will be easier to find 
only
in terms of 
s or
only in terms of 
s, and then find it.
2A)
Use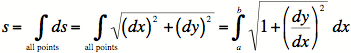 
if 
is
easier.
2B)
Use 
if 
is
easier.
3) Integrate.
Example
#1: Find the length of the curve 
from the point
to the point 
.
1)
It will be easy for this curve to find 
in
terms of 
.
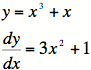
2)
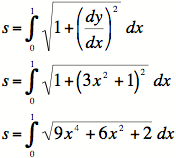
3) Unfortunately, this is not easily integrable. But using our
calculators or computers, we can approximate the answer.
Example #2: Find the circumference of a circle centered about the
origin with radius 7. We should easily be able to check our
answer!
1)
The equation of the circle is 
, so it will
not matter
which derivative we find.
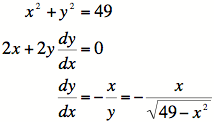
2) To set up the integral, we need to know what to set for our
limits. For closed figures, such as this circle, it is often easiest to
take advantage of symmetry. Notice that we could simply
calculate the top half of the circle's circumference and then
multiply by 2. We could also calculate the first quadrant's worth of
the circle's circumference and multiply by 4. We'll choose the
latter for this problem since that let's us have one of our limits be a
zero.
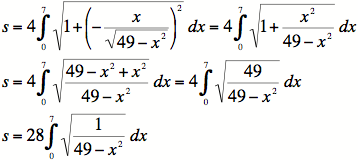
3) To integrate, a simple Trig Sub will suffice (see method 27).
Use the substitution 
And, of course, this is exactly what we expect for a circle
with radius 7.
On to Method 24 - Surface Area