Calculus Methods
24 Surface Area
This method is almost the same as that for arc length (method
23). The reason is that a surface area, at least for surfaces of
revolution, is a differential frustum (a cone with no top). The
result is that instead of height, like we used for our cylindrical
shells (see method 22, Volume), we use the slant height (arc
length).
Since we use a cylinder/frustum, our differential surface area
is 
.
1) Draw picture.
2)
Draw in differential frustum and label 
and 
.
3)
Integrate using 
. Just as in
method
23, pull out the appropriate differential, either 
or 
.
Example:
The curve 
on the interval 
is revolved about
the x-axis. Find the surface area that results.
1) The original graph looks like this:
When revolved about the x-axis, the surface, represented in
2D, will look like this:
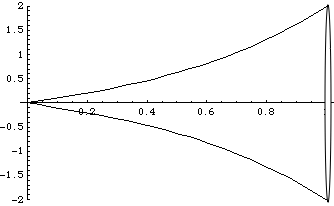
2) Drawing in our differential surface area:
 |
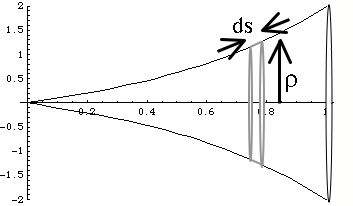3)
We see from the drawing that 
. Some
parts of the
simplification of the integral below are completed in method 23.
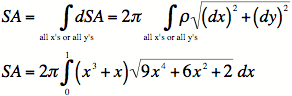
Again, this integral is not easily integrable, so we'll just use the
calculator:
