Calculus Methods
25 Work
First, we must realize that although the true definition of
work is 
, the AP Exam only takes into account
forces
that act either parallel or antiparallel to the direction of
motion. Hence, we may use the equation 
for our
work. The only caveat here is that you must know the relative
directions of the force and distance. If they are in opposite
directions (your hand lowering a rock, for instance, since
your hand is pushing up and the rock is moving down), then
you need to make the work negative.
Second, the real key to performing work problems is to
realize that when we use the product rule, a differential
amount of work is 
.
We then keep one of these
terms, 
or
, constant so that one of these
differentials goes
to zero and we can concentrate solely on the other one.
1) Draw picture!!! Before and after pictures would be extremely
helpful!
2) Determine whether the mass/weight of the object is changing,
or whether it is staying the same.
3)
For constant mass/weight, use 
.
3A) Identify the force involved. Typical forces are:
force
ON a spring, 
force
of gravity between two objects, 
electrostatic
force between two objects, 
3B)
Identify the differential distance: is it 
or
?
3C) Identify your starting and ending values of the variable
found in 3B. It doesn't matter what you label them as long as
you are consistent! If you call the ground 0 and the top of the
building 20, that fine. If you call the ground -15 and the top
of the building 5, that will work as well. Typically it is easiest
to call something 0, but it is not necessary.
3D)
Find 
using the information given in the
problem.
3E)
Find 
in terms of the variable that matches
what
you found in 3B.
3F)
Integrate 
.
3G) Use the proper units in your answer!!!!!
4)
For changing mass/weight, use 
.
4A) Identify the differential weight. You will need to
determine if you were given mass or weight (multiply by g to
go from mass to weight, if given mass). You will also need to
determine if you are looking at differential volume or
differential length (differential area is extremely rare). If
given volume
density, the typical variable to use is 
.
If you
are given a length density, the typical variable to use is 
(think "L" for "length"). Your equation will thus either be:
or 
if
a volume problem, or 
, 
,
,
or 
if a length problem.
4B) Draw on your picture, the differential volume or length.
For a volume problem,
you must now find 
in terms of
either 
or 
.
4C) Identify your starting and ending values of the movement
variable. It doesn't matter what you label them as long as you
are consistent! If you call the ground 0 and the top of the
building 20, that fine. If you call the ground -15 and the top
of the building 5, that will work as well. Typically it is easiest
to call something 0, but it is not necessary.
4D) Using your picture as a guide, find the distance that each
differential volume or length must move, in terms of the
differential direction of the problem. For instance, if the
differential slab that you've drawn in your picture is at
position y and must move up to position 7, then each
differential portion will
move 
, so 
.
4E)
Integrate 
.
4F) Use the proper units in your answer!!!!!
Example #1: The force to compress a spring 6 inches from it's
natural length of 18 inches is 1000 lbs. How much work does it
take to compress the spring another 6 inches?
1)
2) The mass is not changing!
3A)
This is a spring, so the force on the spring is 
.
3B)
We can say it is being compressed 
.
3C) Our starting values will be 0 and 12, since the question is
asking us how much work is required to compress the spring
from 0 difference (at the natural length) to 12 difference (12
inches compressed).
3D)
We can find 
from the given information,
since we
know the force is 1000 lbs. when x is 6 inches:
3E)
3F)
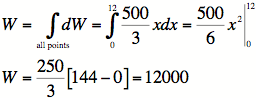
3G) We are using pounds and inches, so the answer is
.
We could also call it 
to be more
conventional.
Example #2: A chain that is five pounds per foot is 20 feet long
and lying on the ground. You are going to raise the chain so that
the top of the chain is 30 ft off of the ground and the rest of the
chain is hanging straight down. How much work is required?
1)
2) The mass of what we are lifting changes as we lift it, so we will
be using 
.
4A) The density is already given to us in terms of weight
(lbs.), so we do not need to multiply by g. Our equation, since
we are moving in the y-direction, is 
.
4B)
4C)
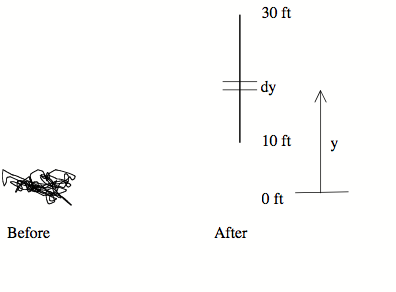
Based
on our labeling, the y-values vary from 
to
.
4D) Each piece of the chain must move from the ground
(which we have labeled 0) up to it's final resting place of y, so
for each differential weight, we find it
must move a distance 
.
4E)
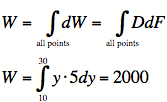
4F)
We are dealing with feet and pounds, so our work is 
.
Example #3: A spherical tank, 9 meters in radius, is half-full of oil
(0.9 kg/l3). Find the work to pump all of the oil out of the top of
the tank.
1)
2) In this case, the amount of weight we must lift out of the tank
changes: we will look at lifting a horizontal discs of oil out. Since
the size of the disc changes, our weight changes.
4A) The density is given in terms of mass, so must multiply
by g to get weight. Also, the density is given per liter,
whereas our linear measurement is in meters, so we will also
convert liters to cubic meters.
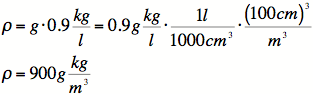
4B)
It is fairly common to put 
on the
bottom of an
object, but it is not necessary.
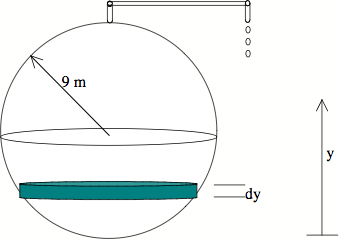
The problem now is to determine how much weight a
differential volume element is.
For a disc of radius 
, we
know the
differential volume is 
. But we
need a way
to find 
in terms of 
. The best way to do this is do draw
the
appropriate triangle:
Since
we have a right triangle, we can see that 
.
So we have an equation for 
and we have
our differential
volume in terms of 
:
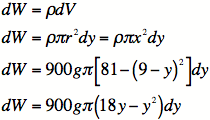
4C) From our picture, the y-values of the discs range from
to 
.
4D) Again from our picture, each slab of oil needs to move
up a distance 
. This makes it so that the disc lying
on
top moves 9 meters and the bottom drop moves 18 meters.
4E)
4F) All of our units are meters and kilograms, so our unit of
work is Newtons. 
Try
re-working the problem with 
at different
positions!