Calculus Methods
31 Generating Geometric Power Series
The key to converting certain types of functions into power
series is to use the definition of a Geometric Power Series:
1) If the denominator can be factored, use the method of
separating partial fractions (see method 03) to split the single
fraction into multiple fractions.
2) You will either be told about what value the series should be
found, or you can decide for yourself. In
either case, you will have 
.
3) For each fraction, you will have either a denominator that looks
like 
. If you have some more complicated
factors than this,
revert to using the Taylor Series (see method 32) form of the
expansion.
4) You must arrange
for the denominator to look like 
where. This will either take adding a zero, or completing the
square and THEN adding a zero. If you
subtract 
from the 
, you
should note that you must also add
to the entire denominator to
cancel it out. Your new denominator is
thus 
.
If we
then factor out 
, our denominator has
the form
. This may look
complicated with variables, but
when we deal with numbers, it's typically not so bad.
5) The factor of 
outside is simply a
coefficient. The 
is what we will call 
.
6) Use the formula 
to write your power
series.
7) Don't forget that a power series is never fully dressed without a
smile (and an Interval of Convergence (see method 30)). The nice
part about geometric series, is that they always diverge at their
endpoints, so we don't have to test them.
Example: Find the
power series for the function 
centered about 
.
1) The denominator is already factored.
2)
3) We already have a
denominator in the correct form, 
.
4) We need to add 3
just to the 
. Our new
function looks like:
. You can see that we
have
essentially "done" nothing, since we have subtracted 6 and added 6.
Continuing,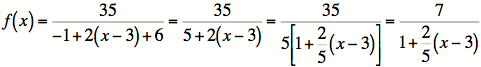 
.
Finally, we need to make sure that we are subtracting on the
bottom.
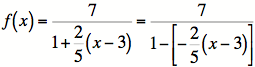
5) So now we see that 
.
6)
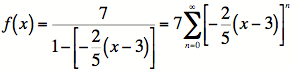
It is
customary, however, to keep any 
separate, and to
keep 
separate as well. Our
answer, then, is
or 
.
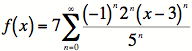Either form is
common.
7) Using
method 30, we find that the Interval of Convergence is 
.
The final answer is
thus 
, 
.
On to Method 32 - Generating Taylor Series and Taylor Polynomials