Calculus Methods
09 Finding "Other" Points of Inflection
Some points of inflection are also critical points.
When testing any critical points (see method 08),
the second derivative test will fail, and you must
make a sign chart to see where the derivative
changes its sign about a critical number and where
the derivative keeps its sign. When the derivative
keeps its sign about a critical number, that critical
point is a point of inflection.
However, there are other points of inflection. Any
time when the second derivative is equal to zero at
a point other than a critical point, that point MUST
be a point of inflection.
So the rule is: if the second derivative equals zero at
a given point, then a) if the point is a critical point,
make a sign chart to see if it is an extremum or a
point of inflection, and b) if the point is not a
critical point, it must be a point of inflection.
1) Find the first and second derivatives.
2) Use method 08 to determine which critical
numbers are extrema and which are points of
inflection.
3) Set the second derivative equal to zero and solve
for the x values. Any value of x that is not also a
critical number is the x-coordinate of a point of
inflection.
Example #1: Find all relative extrema and points of
inflection of the function 
.
1)
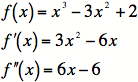
2)
Critical numbers occur where 
is either
zero
or undefined. This happens when 
. Testing
these to critical numbers with the second derivative
test, we find
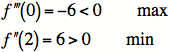
So
a maximum occurs at 
and a minimum occurs
at 
. There are no critical numbers that
are
points of inflection.
3) So the only points of inflection that exist for this
function must be "other" points of inflection, where
the second derivative equals zero.
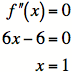
Since
must be the x-coordinate of a point of
inflection, we have a point of inflection must be
.
Example #2: Find all relative extrema and points of
inflection of the function 
.
1)
.
2) Critical numbers:
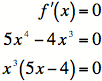
So
the critical numbers are 
. Using the
second
derivative test, we find 
, so the
second
derivative test fails. Using a sign chart, however,
lets us find that the
point when 
the function is a
maximum and when 
the function is a
minimum. So there is a maximum at 
and a
minimum at 
.
3) To find other points of inflection, we must set the
second derivative equal to zero.
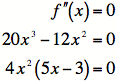
So
the second derivative equals zero when 
.
We
can ignore 
, since it is also a
critical
number, so we already know what happens there.
That means that 
must correspond to a point of
inflection,
at 
.
On to Method 10 - Limits at Infinity